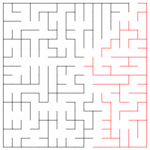
Most people know that you can always solve a maze (eventually) by turning left. Here’s a more visual solution to the maze problem which I developed for a elementary school class at Waseca Montessori School in Athens, Georgia. Instead of thinking about the maze, think about the walls of the maze: if there’s a path through, that path has to divide the walls into two disconnected pieces. If you color in the walls differently, the solution to the maze becomes obvious!
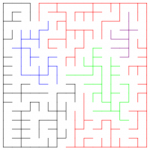
Of course, you can make an even harder maze, with several different solutions, by adding some more connected pieces to the maze (with more colors, of course). Here’s one with 5 components instead of two.
I made a bunch of mazes with Mathematica for the students to try, which you can print out as PDF files: Level 2 Maze, Level 2 Maze, Level 3 Maze, Level 4 Maze, Level 5 Maze, Level 6 Maze, Level 13 Maze, Level 16 Maze.
You can play with the demonstration by downloading Coloring Mazes (CDF) which is a file in the Wolfram Computable Document Format, which is really pretty neat! This is now also available as part of the Wolfram Demonstrations Project.