The Flocktree is a sculptural installation of a flock of pigeons cast in an expanding urethane foam supported and grouped by a collection of nesting aluminum frames. The interplay between the rigorous order imposed by the frames and the fluid organic shape of the flock raises questions about the way the viewer makes sense of collections of objects. The groupings of birds created by the frames form an octree structure.
The Flocktree was made possible by the financial support of the ICE program at UGA and installed in the courtyard at the Floor Group at 159 Oneta Street in Athens, GA. The Flocktree was created in collaboration with my brother Luke Cantarella a scenic designer and artist living in Brooklyn, NY.
Subdividing a flock of birds
The Flocktree structure divides a group of 17 bird sculptures into 6 groups by grouping them into front/back, left/right, and top/bottom groups, then enclosing each subgroup (such as the top/right/front) group in an aluminum frame. The entire flock is contained in a larger frame as shown below.
This process for dividing objects into groups is used in computational geometry and computer graphics to quickly process large collections of geometric objects.
Building a Frame
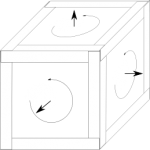
Constructing the frames for the boxes poses an interesting challenge: how to build the best box possible from angle stock without mitering and welding it? Each of the corners are constructed in a triple-overlapping pattern shown in the gallery below. This means that around a face of each box, the pieces overlap in a spiral pattern, as shown in the middle frame. These spirals can be right-handed or left-handed. Can we pick a direction for the spiral on each frame so that they are all compatible?
As the pictures show, all of the spirals are compatible as long as each one points outward from the cube. In a frame built like this, all the corners are the same. In practice, this makes the cube design particularly strong and accurate, since each piece of angle stock is bent just a bit out of shape and the pieces all press together symmetrically at the corners.
This design is a simple example of a mathematical concept called orientability. A surface, like the cube is said to be orientable if on each face you can choose an outward direction so that all of these directions are compatible. Any surface like this can be built with the spiraling frames above. On the other hand, a nonorientable surface, like a mobius strip, couldn’t have been built this way!